You can run this notebook in a live session or view it on Github.

Implications of `verify(dim)`#

This demo demonstrates how setting dim in PerfectModelEnsemble.verify() and HindcastEnsemble.verify() alters the research question and prediction skill obtained, especially for spatial fields.

What’s the purpose of dim?

dim is designed the same way as in xarray.Dataset.mean(). A given metric is calculated over dimension dim, i.e. the result does not contain dim anymore. dim can be a string or list of strings.

3 ways to calculate aggregated prediction skill

Spatially aggregate first, then verify
verify on each grid point, then aggregate spatially
verify over spatial, member and initialization directly

# linting
%load_ext nb_black
%load_ext lab_black

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 2
      1 # linting
----> 2 get_ipython().run_line_magic('load_ext', 'nb_black')
      3 get_ipython().run_line_magic('load_ext', 'lab_black')

File ~/checkouts/readthedocs.org/user_builds/climpred/conda/latest/lib/python3.9/site-packages/IPython/core/interactiveshell.py:2456, in InteractiveShell.run_line_magic(self, magic_name, line, _stack_depth)
   2454     kwargs['local_ns'] = self.get_local_scope(stack_depth)
   2455 with self.builtin_trap:
-> 2456     result = fn(*args, **kwargs)
   2458 # The code below prevents the output from being displayed
   2459 # when using magics with decorator @output_can_be_silenced
   2460 # when the last Python token in the expression is a ';'.
   2461 if getattr(fn, magic.MAGIC_OUTPUT_CAN_BE_SILENCED, False):

File ~/checkouts/readthedocs.org/user_builds/climpred/conda/latest/lib/python3.9/site-packages/IPython/core/magics/extension.py:33, in ExtensionMagics.load_ext(self, module_str)
     31 if not module_str:
     32     raise UsageError('Missing module name.')
---> 33 res = self.shell.extension_manager.load_extension(module_str)
     35 if res == 'already loaded':
     36     print("The %s extension is already loaded. To reload it, use:" % module_str)

File ~/checkouts/readthedocs.org/user_builds/climpred/conda/latest/lib/python3.9/site-packages/IPython/core/extensions.py:76, in ExtensionManager.load_extension(self, module_str)
     69 """Load an IPython extension by its module name.
     70 
     71 Returns the string "already loaded" if the extension is already loaded,
     72 "no load function" if the module doesn't have a load_ipython_extension
     73 function, or None if it succeeded.
     74 """
     75 try:
---> 76     return self._load_extension(module_str)
     77 except ModuleNotFoundError:
     78     if module_str in BUILTINS_EXTS:

File ~/checkouts/readthedocs.org/user_builds/climpred/conda/latest/lib/python3.9/site-packages/IPython/core/extensions.py:91, in ExtensionManager._load_extension(self, module_str)
     89 with self.shell.builtin_trap:
     90     if module_str not in sys.modules:
---> 91         mod = import_module(module_str)
     92     mod = sys.modules[module_str]
     93     if self._call_load_ipython_extension(mod):

File ~/checkouts/readthedocs.org/user_builds/climpred/conda/latest/lib/python3.9/importlib/__init__.py:127, in import_module(name, package)
    125             break
    126         level += 1
--> 127 return _bootstrap._gcd_import(name[level:], package, level)

File <frozen importlib._bootstrap>:1030, in _gcd_import(name, package, level)

File <frozen importlib._bootstrap>:1007, in _find_and_load(name, import_)

File <frozen importlib._bootstrap>:984, in _find_and_load_unlocked(name, import_)

ModuleNotFoundError: No module named 'nb_black'

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import xarray as xr

import climpred

climpred.set_options(PerfectModel_persistence_from_initialized_lead_0=True)

<climpred.options.set_options at 0x107023be0>

sample spatial initialized ensemble data and nomenclature#

We also have some sample output that contains gridded data on MPIOM grid:

initialized3d: The initialized ensemble dataset with
- members (1, … , 4) denoted by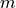 $m$
- inits (initialization years: 3014, 3061, 3175, 3237) denoted by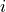 $i$
- lead years (1, …, 5) denoted by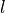 $l$ .
- x and j (think as longitude and latitude): spatial dimensions denotes by $s$ .
control3d: The control dataset spanning over time (3000, …, 3049) [not used here].

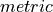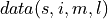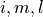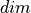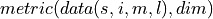In PerfectModelEnsemble.verify(), we calculate a $metric$ on $data(s,i,m,l)$ containing spatial dimensions $s$ and ensemble dimension $i,m,l$ over dimensions $dim$ denoted by $metric(data(s,i,m,l), dim)$ .

# Sea surface temperature
initialized3d = climpred.tutorial.load_dataset("MPI-PM-DP-3D")
control3d = climpred.tutorial.load_dataset("MPI-control-3D")
v = "tos"
initialized3d["lead"].attrs = {"units": "years"}

# Create climpred PerfectModelEnsemble object.
pm = (
    climpred.PerfectModelEnsemble(initialized3d).add_control(control3d)
    # .generate_uninitialized() # needed for uninitialized in reference
)

/Users/aaron.spring/Coding/climpred/climpred/utils.py:195: UserWarning: Assuming annual resolution starting Jan 1st due to numeric inits. Please change ``init`` to a datetime if it is another resolution. We recommend using xr.CFTimeIndex as ``init``, see https://climpred.readthedocs.io/en/stable/setting-up-data.html.
  warnings.warn(
/Users/aaron.spring/mambaforge/envs/climpred-dev/lib/python3.10/site-packages/xarray/coding/times.py:351: FutureWarning: Index.ravel returning ndarray is deprecated; in a future version this will return a view on self.
  sample = dates.ravel()[0]
/Users/aaron.spring/Coding/climpred/climpred/utils.py:195: UserWarning: Assuming annual resolution starting Jan 1st due to numeric inits. Please change ``init`` to a datetime if it is another resolution. We recommend using xr.CFTimeIndex as ``init``, see https://climpred.readthedocs.io/en/stable/setting-up-data.html.
  warnings.warn(
/Users/aaron.spring/mambaforge/envs/climpred-dev/lib/python3.10/site-packages/xarray/coding/times.py:351: FutureWarning: Index.ravel returning ndarray is deprecated; in a future version this will return a view on self.
  sample = dates.ravel()[0]

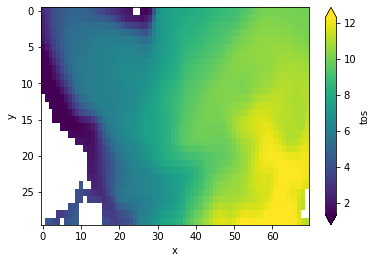
subselecting North Atlantic#

pm = pm.isel(x=slice(80, 150), y=slice(40, 70))
pm.get_initialized().mean(["lead", "member", "init"])[v].plot(
    yincrease=False, robust=True
)

<matplotlib.collections.QuadMesh at 0x14cbe2f50>

../../_images/9bdbfb5a667f7442f012f54b111597f3bd1b780cb6f979f9127a16f7e1fff188.png

verify_kwargs = dict(
    metric="pearson_r",  # 'rmse'
    comparison="m2m",
    reference=["persistence", "climatology"],  # "uninitialized",
    skipna=True,
)
dim = ["init", "member"]
spatial_dims = ["x", "y"]

Here, we use the anomaly correlation coefficient climpred.metrics._pearson_r(). Also try root-mean-squared-error climpred.metrics._rmse().

Spatial aggregate first, then `verify`#

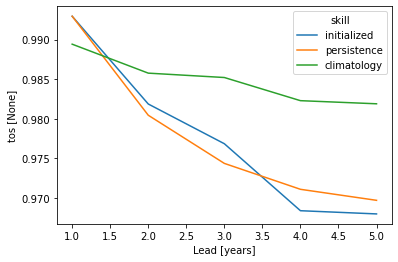
Here, we first average the raw ensemble data over the spatial_dims, i.e. creating North Atlantic averaged SST timeseries. On this timeseries, we calculate the prediction skill with PerfectModelEnsemble.verify().

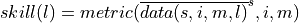
$skill(l) = metric(\overline{data(s,i,m,l)}^s, i, m)$

where 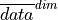$\overline{data}^{dim}$ represents the average of 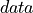$data$ over dimension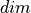 $dim$

This approach answers the question: “What’s the prediction skill of SSTs, which were averaged before over the North Atlantic? What is the skill at predicting average [metric] in [domain]?”

Used in Séférian et al. [2018], Spring and Ilyina [2020], Pohlmann et al. [2004].

Recommended by Goddard et al. [2013] section 2.1.4:

“We advocate verifying on at least two spatial scales: (1) the observational grid scales to which the model data is interpolated, and (2) smoothed or regional scales. The latter can be accomplished by suitable spatial-smoothing algorithms, such as simple averages or spectral filters.”

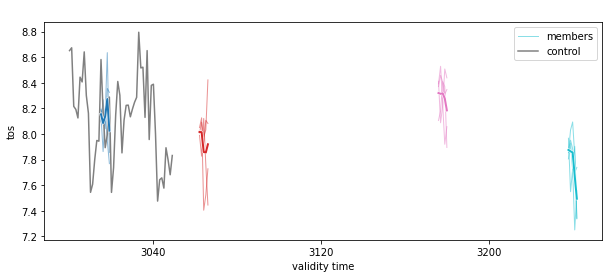
pm_aggregated = pm.mean(spatial_dims)
# see the NA SST timeseries
pm_aggregated.plot(show_members=True)

<AxesSubplot:title={'center':' '}, xlabel='validity time', ylabel='tos'>

../../_images/082f11fda86654e81db932accf9132276a2d04acc19b144fc5599b296add53d3.png

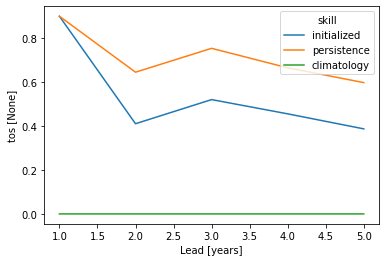
pm_aggregated_skill = pm_aggregated.verify(dim=dim, **verify_kwargs)
pm_aggregated_skill[v].plot(hue="skill")

/Users/aaron.spring/Coding/climpred/climpred/classes.py:1597: UserWarning: Calculate persistence from lead=1 instead of lead=0 (recommended).
  warnings.warn(

[<matplotlib.lines.Line2D at 0x14d4628f0>,
 <matplotlib.lines.Line2D at 0x14d4631c0>,
 <matplotlib.lines.Line2D at 0x14b69cf10>]

../../_images/1053bc5614e0df55ef1903fb660a50f52250dff35a9298524ec0d5955df86ec5.png

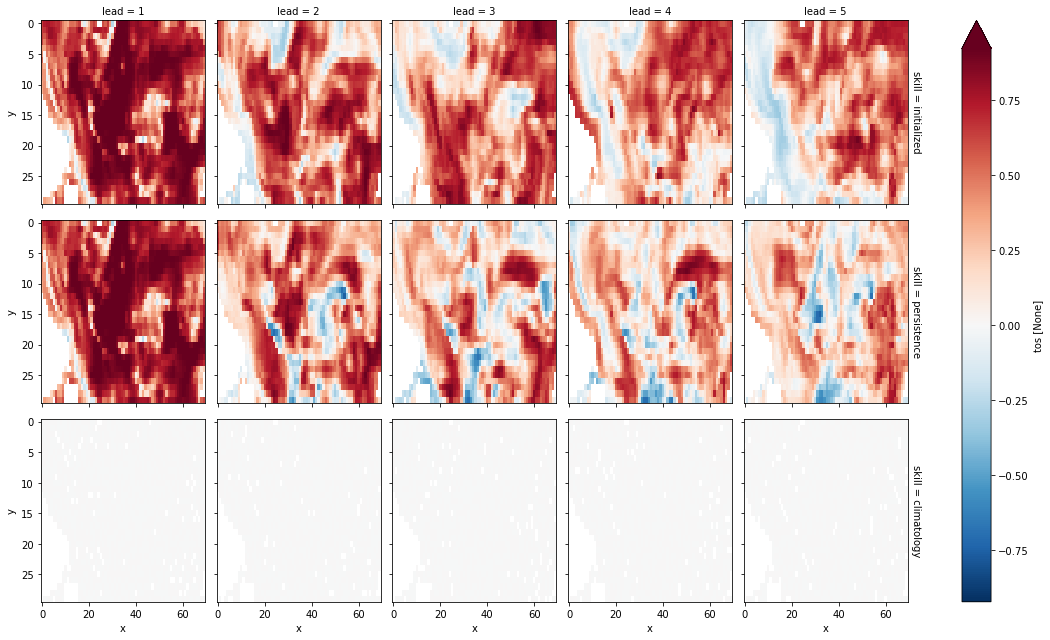
`verify` on each grid point, then aggregate#

Here, we first calculate prediction skill with PerfectModelEnsemble.verify() and then average the SST skill over the North Atlantic region.

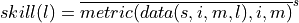
$skill(l) = \overline{metric(data(s,i,m,l), i, m)}^s$

This approach answers the question: “What’s the prediction skill of North Altantic SST grid points averaged afterwards? What is the average skill of predicting [metric] in [domain]?”

Used in Frölicher et al. [2020].

grid_point_skill = pm.verify(dim=dim, **verify_kwargs)
grid_point_skill[v].plot(col="lead", row="skill", robust=True, yincrease=False)

/Users/aaron.spring/Coding/climpred/climpred/classes.py:1597: UserWarning: Calculate persistence from lead=1 instead of lead=0 (recommended).
  warnings.warn(

<xarray.plot.facetgrid.FacetGrid at 0x14d8f1180>

../../_images/f8b86988eb5a90c81dc67c201ea48e776c70aff969a9c3f961aa74d312a6df70.png

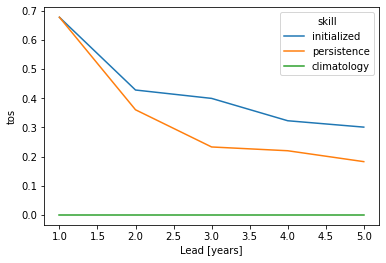
grid_point_skill_aggregated = grid_point_skill.mean(spatial_dims)
grid_point_skill_aggregated[v].plot(hue="skill")
plt.show()

../../_images/61a970f976f6f65ff7e4ea057cc2838a0c08b4749d8781208f80f6b951a2e84c.png

`verify` over each grid point, `member` and `init`ialization directly#

Here, we directly calculate prediction skill with PerfectModelEnsemble.verify() over spatial_dims, member and init.

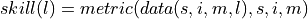
$skill(l) = metric(data(s,i,m,l), s, i, m)$

This approach answers the question: What’s the prediction skill of the North Atlantic SST pattern (calculated over all members and inits)? What is the spatial skill of predicting [metric] over [domain]?

Used in Becker et al. [2014], Fransner et al. [2020].

skill_all_at_once = pm.verify(dim=dim + spatial_dims, **verify_kwargs)
skill_all_at_once[v].plot(hue="skill")
plt.show()

/Users/aaron.spring/Coding/climpred/climpred/classes.py:1597: UserWarning: Calculate persistence from lead=1 instead of lead=0 (recommended).
  warnings.warn(

../../_images/8b4407ee21c3be349ce196900df4fbc1e3fc53a06e2d1f802b5763136a3fa903.png

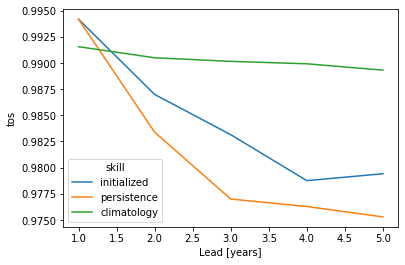
This approach yields very similar results to first calculating prediction skill over the spatial_dims, i.e. calculating a pattern correlation and then doing a mean over ensemble dimensions member and init.

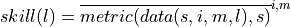
$skill(l) = \overline{metric(data(s,i,m,l), s)}^{i,m}$

skill_spatial_then_ensemble_mean = pm.verify(dim=spatial_dims, **verify_kwargs).mean(
    dim
)
skill_spatial_then_ensemble_mean[v].plot(hue="skill")
plt.show()

/Users/aaron.spring/Coding/climpred/climpred/classes.py:1597: UserWarning: Calculate persistence from lead=1 instead of lead=0 (recommended).
  warnings.warn(

../../_images/b29204c56dc302acd39eb7383de883542c53d68ef5f90a85520575b7031fee72.png

Summary#

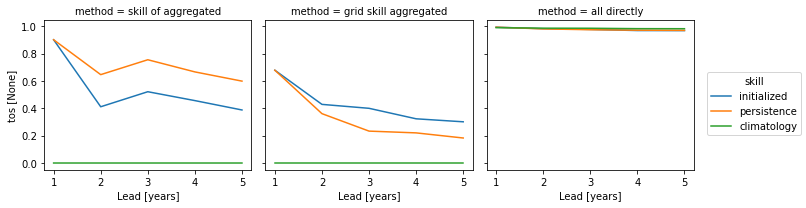
The three approaches yield very different results based on the dim keyword. Make you choose dim according to the question you want to answer. And always compare your initialized skill to the reference skills, which also heavily depend on dim. The small details matter a lot!

skills = xr.concat(
    [pm_aggregated_skill, grid_point_skill_aggregated, skill_all_at_once], "method"
).assign_coords(method=["skill of aggregated", "grid skill aggregated", "all directly"])

skills[v].plot(hue="method", col="skill")

<xarray.plot.facetgrid.FacetGrid at 0x14d7f4460>

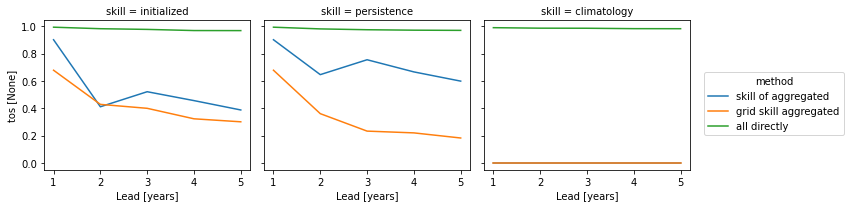
../../_images/42fa124b97b90a715bc623938ff7659b97ba8ccc0ec26904269871e05873179e.png

skills[v].plot(col="method", hue="skill")

<xarray.plot.facetgrid.FacetGrid at 0x14df5b970>

../../_images/2aceca4e8268e806aafe370f74fc7a7e35bb44650fcbde9a11fb0a313d7c6032.png

References#

[1]

Emily Becker, Huug van den Dool, and Qin Zhang. Predictability and Forecast Skill in NMME. Journal of Climate, 27(15):5891–5906, August 2014. doi:10.1175/JCLI-D-13-00597.1.

[2]

Filippa Fransner, François Counillon, Ingo Bethke, Jerry Tjiputra, Annette Samuelsen, Aleksi Nummelin, and Are Olsen. Ocean Biogeochemical Predictions—Initialization and Limits of Predictability. Frontiers in Marine Science, 2020. doi:10/gg22rr.

[3]

Thomas L. Frölicher, Luca Ramseyer, Christoph C. Raible, Keith B. Rodgers, and John Dunne. Potential predictability of marine ecosystem drivers. Biogeosciences, 17(7):2061–2083, April 2020. doi:10/ggr9mb.

[4]

L. Goddard, A. Kumar, A. Solomon, D. Smith, G. Boer, P. Gonzalez, V. Kharin, W. Merryfield, C. Deser, S. J. Mason, B. P. Kirtman, R. Msadek, R. Sutton, E. Hawkins, T. Fricker, G. Hegerl, C. a. T. Ferro, D. B. Stephenson, G. A. Meehl, T. Stockdale, R. Burgman, A. M. Greene, Y. Kushnir, M. Newman, J. Carton, I. Fukumori, and T. Delworth. A verification framework for interannual-to-decadal predictions experiments. Climate Dynamics, 40(1-2):245–272, January 2013. doi:10/f4jjvf.

[5]

Holger Pohlmann, Michael Botzet, Mojib Latif, Andreas Roesch, Martin Wild, and Peter Tschuck. Estimating the Decadal Predictability of a Coupled AOGCM. Journal of Climate, 17(22):4463–4472, November 2004. doi:10/d2qf62.

[6]

Aaron Spring and Tatiana Ilyina. Predictability Horizons in the Global Carbon Cycle Inferred From a Perfect-Model Framework. Geophysical Research Letters, 47(9):e2019GL085311, 2020. doi:10/ggtbv2.

[7]

Roland Séférian, Sarah Berthet, and Matthieu Chevallier. Assessing the Decadal Predictability of Land and Ocean Carbon Uptake. Geophysical Research Letters, March 2018. doi:10/gdb424.

Implications of verify(dim)

Contents

Implications of `verify(dim)`#

sample spatial initialized ensemble data and nomenclature#

subselecting North Atlantic#

Spatial aggregate first, then `verify`#

`verify` on each grid point, then aggregate#

`verify` over each grid point, `member` and `init`ialization directly#

Summary#

References#

Implications of verify(dim)

Contents

Implications of verify(dim)#

sample spatial initialized ensemble data and nomenclature#

subselecting North Atlantic#

Spatial aggregate first, then verify#

verify on each grid point, then aggregate#

verify over each grid point, member and initialization directly#

Summary#

References#

Implications of `verify(dim)`#

Spatial aggregate first, then `verify`#

`verify` on each grid point, then aggregate#

`verify` over each grid point, `member` and `init`ialization directly#