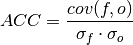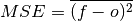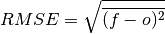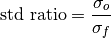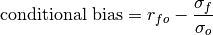Metrics¶

All high-level functions have an optional metric argument that can be called to determine which metric is used in computing predictability (potential predictability or prediction skill).

Note

We use the phrase ‘observations’ o here to refer to the ‘truth’ data to which we compare the forecast f. These metrics can also be applied in reference to a control simulation, reconstruction, observations, etc. This would just change the resulting score from referencing skill to referencing potential predictability.

Internally, all metric functions require forecast and reference as inputs. The dimension dim is set by climpred.prediction.compute_hindcast() or climpred.prediction.compute_perfect_model() to specify over which dimensions the metric is applied. See Comparisons.

Deterministic¶

Deterministic metrics quantify the level to which the forecast predicts the observations. These metrics are just a special case of probabilistic metrics where a value of 100% is assigned to the forecasted value [Jolliffe2011].

Core Metrics¶

Anomaly Correlation Coefficient (ACC)¶

keyword: 'pearson_r','pr','acc'

A measure of the linear association between the forecast and observations that is independent of the mean and variance of the individual distributions [Jolliffe2011]. climpred uses the Pearson correlation coefficient.

climpred.metrics._pearson_r(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate the Anomaly Correlation Coefficient (ACC).

$ACC = \frac{cov(f, o)}{\sigma_{f}\cdot\sigma_{o}}$

Note

Use metric pearson_r_p_value to get the corresponding pvalue.

Range:

perfect: 1
min: -1

See also

xskillscore.pearson_r
xskillscore.pearson_r_p_value

Mean Squared Error (MSE)¶

keyword: 'mse'

The average of the squared difference between forecasts and observations. This incorporates both the variance and bias of the estimator.

climpred.metrics._mse(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate the Mean Sqaure Error (MSE).

$MSE = \overline{(f - o)^{2}}$

Range:

perfect: 0
min: 0
max: ∞

See also

xskillscore.mse

Root Mean Square Error (RMSE)¶

keyword: 'rmse'

The square root of the average of the squared differences between forecasts and observations [Jolliffe2011]. It puts a greater influence on large errors than small errors, which makes this a good choice if large errors are undesirable or one wants to be a more conservative forecaster.

climpred.metrics._rmse(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate the Root Mean Sqaure Error (RMSE).

$RMSE = \sqrt{\overline{(f - o)^{2}}}$

Range:

perfect: 0
min: 0
max: ∞

See also

xskillscore.rmse

Mean Absolute Error (MAE)¶

keyword: 'mae'

The average of the absolute differences between forecasts and observations [Jolliffe2011]. A more robust measure of forecast accuracy than root mean square error or mean square error which is sensitive to large outlier forecast errors [EOS].

climpred.metrics._mae(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate the Mean Absolute Error (MAE).

$MSE = \overline{(f - o)^{2}}$

Range:

perfect: 0
min: 0
max: ∞

See also

xskillscore.mae

Derived Metrics¶

Distance-based metrics like mse can be normalized to 1. The normalization factor depends on the comparison type choosen, eg. the distance between an ensemble member and the ensemble mean is half the distance of an ensemble member with other ensemble members. (see climpred.metrics._get_norm_factor()).

Normalized Mean Square Error (NMSE)¶

keyword: 'nmse','nev'

climpred.metrics._nmse(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate Normalized MSE (NMSE) = Normalized Ensemble Variance (NEV).

$NMSE = NEV = \frac{MSE}{\sigma^2_{o} \cdot fac}$

Parameters:	forecast () – reference* () – dim* () – dimension to apply metric to comparison* () – name comparison needed for normalization factor (required to be added via *metric_kwargs)

Range:

0: perfect forecast: 0
0 - 1: better than climatology forecast
> 1: worse than climatology forecast

References

Griffies, S. M., and K. Bryan. “A Predictability Study of Simulated North Atlantic Multidecadal Variability.” Climate Dynamics 13, no. 7–8 (August 1, 1997): 459–87. https://doi.org/10/ch4kc4.

Normalized Mean Absolute Error (NMAE)¶

keyword: 'nmae'

climpred.metrics._nmae(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Normalized Ensemble Mean Absolute Error metric.

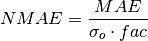
$NMAE = \frac{MAE}{\sigma_{o} \cdot fac}$

Parameters:	forecast () – reference* () – dim* () – dimension to apply metric to comparison* () – name comparison needed for normalization factor (required to be added via *metric_kwargs)

Range:

0: perfect forecast: 0
0 - 1: better than climatology forecast
> 1: worse than climatology forecast

References

Griffies, S. M., and K. Bryan. “A Predictability Study of Simulated North Atlantic Multidecadal Variability.” Climate Dynamics 13, no. 7–8 (August 1, 1997): 459–87. https://doi.org/10/ch4kc4.

Normalized Root Mean Square Error (NRMSE)¶

keyword: 'nrmse'

climpred.metrics._nrmse(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Normalized Root Mean Square Error (NRMSE) metric.

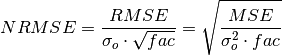
$NRMSE = \frac{RMSE}{\sigma_{o} \cdot \sqrt{fac} } = \sqrt{ \frac{MSE}{ \sigma^2_{o} \cdot fac} }$

Parameters:	forecast () – reference* () – dim* () – dimension to apply metric to comparison* () – name comparison needed for normalization factor (required to be added via *metric_kwargs)

Range:

0: perfect forecast
0 - 1: better than climatology forecast
> 1: worse than climatology forecast

References

Bushuk, Mitchell, Rym Msadek, Michael Winton, Gabriel Vecchi, Xiaosong Yang, Anthony Rosati, and Rich Gudgel. “Regional Arctic Sea–Ice Prediction: Potential versus Operational Seasonal Forecast Skill.” Climate Dynamics, June 9, 2018. https://doi.org/10/gd7hfq.
Hawkins, Ed, Steffen Tietsche, Jonathan J. Day, Nathanael Melia, Keith Haines, and Sarah Keeley. “Aspects of Designing and Evaluating Seasonal-to-Interannual Arctic Sea-Ice Prediction Systems.” Quarterly Journal of the Royal Meteorological Society 142, no. 695 (January 1, 2016): 672–83. https://doi.org/10/gfb3pn.

Mean Square Skill Score (MSSS)¶

keyword: 'msss','ppp'

climpred.metrics._ppp(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Prognostic Potential Predictability (PPP) metric.

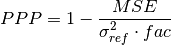
$PPP = 1 - \frac{MSE}{ \sigma^2_{ref} \cdot fac}$

Parameters:	forecast () – reference* () – dim* () – dimension to apply metric to comparison* () – name comparison needed for normalization factor (required to be added via *metric_kwargs)

Range:

1: perfect forecast
positive: better than climatology forecast
negative: worse than climatology forecast

References

Griffies, S. M., and K. Bryan. “A Predictability Study of Simulated North Atlantic Multidecadal Variability.” Climate Dynamics 13, no. 7–8 (August 1, 1997): 459–87. https://doi.org/10/ch4kc4.
Pohlmann, Holger, Michael Botzet, Mojib Latif, Andreas Roesch, Martin Wild, and Peter Tschuck. “Estimating the Decadal Predictability of a Coupled AOGCM.” Journal of Climate 17, no. 22 (November 1, 2004): 4463–72. https://doi.org/10/d2qf62.
Bushuk, Mitchell, Rym Msadek, Michael Winton, Gabriel Vecchi, Xiaosong Yang, Anthony Rosati, and Rich Gudgel. “Regional Arctic Sea–Ice Prediction: Potential versus Operational Seasonal Forecast Skill. Climate Dynamics, June 9, 2018. https://doi.org/10/gd7hfq.

Unbiased ACC¶

keyword: 'uacc'

climpred.metrics._uacc(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate Bushuk’s unbiased ACC (uACC).

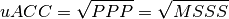
$uACC = \sqrt{PPP} = \sqrt{MSSS}$

Range:

1: perfect
0 - 1: better than climatology

References

Bushuk, Mitchell, Rym Msadek, Michael Winton, Gabriel Vecchi, Xiaosong Yang, Anthony Rosati, and Rich Gudgel. “Regional Arctic Sea–Ice Prediction: Potential versus Operational Seasonal Forecast Skill. Climate Dynamics, June 9, 2018. https://doi.org/10/gd7hfq.

Murphy decomposition metrics¶

[Murphy1988] relates the MSSS with ACC and unconditional bias.

Standard Ratio¶

keyword: 'std_ratio'

climpred.metrics._std_ratio(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate the ratio of standard deviations of reference over forecast.

$\text{std ratio} = \frac{\sigma_o}{\sigma_f}$

References

https://www-miklip.dkrz.de/about/murcss/

Unconditional Bias¶

keyword: 'bias', 'unconditional_bias', 'u_b'

climpred.metrics._bias(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate unconditional bias.

$bias = f - o$

Range:

pos: positive bias
neg: negative bias
perfect: 0

References

Bias Slope¶

keyword: 'bias_slope'

climpred.metrics._bias_slope(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate bias slope between reference and forecast standard deviations.

$\text{bias slope}= r_{fo} \cdot \text{std ratio}$

References

https://www-miklip.dkrz.de/about/murcss/

Conditional Bias¶

keyword: 'conditional_bias', c_b'

climpred.metrics._conditional_bias(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate the conditional bias between forecast and reference.

$\text{conditional bias} = r_{fo} - \frac{\sigma_f}{\sigma_o}$

References

https://www-miklip.dkrz.de/about/murcss/

Murphy’s Mean Square Skill Score¶

keyword: 'msss_murphy'

climpred.metrics._msss_murphy(forecast, reference, dim='svd', **metric_kwargs)[source]¶

Calculate Murphy’s Mean Square Skill Score (MSSS).

$MSSS_{Murphy} = r_{fo}^2 - [\text{conditional bias}]^2 - [\frac{\text{(unconditional) bias}}{\sigma_o}]^2$

References

https://www-miklip.dkrz.de/about/murcss/
Murphy, Allan H. “Skill Scores Based on the Mean Square Error and Their Relationships to the Correlation Coefficient.” Monthly Weather Review 116, no. 12 (December 1, 1988): 2417–24. https://doi.org/10/fc7mxd.

Probabilistic¶

keyword: 'crps'

climpred.metrics._crps(forecast, reference, **metric_kwargs)[source]¶

Continuous Ranked Probability Score (CRPS) is the probabilistic MSE.

Range:

perfect: 0
min: 0
max: ∞

References

Matheson, James E., and Robert L. Winkler. “Scoring Rules for Continuous Probability Distributions.” Management Science 22, no. 10 (June 1, 1976): 1087–96. https://doi.org/10/cwwt4g.

See also

properscoring.crps_ensemble
xskillscore.crps_ensemble

keyword: 'crpss'

climpred.metrics._crpss(forecast, reference, **metric_kwargs)[source]¶

Continuous Ranked Probability Skill Score

Note

When assuming a gaussian distribution of forecasts, use default gaussian=True. If not gaussian, you may specify the distribution type, xmin/xmax/tolerance for integration (see xskillscore.crps_quadrature).

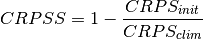
$CRPSS = 1 - \frac{CRPS_{init}}{CRPS_{clim}}$

Parameters:	forecast () – reference* () – gaussian* () – Assuming gaussian distribution for baseline skill. Default: True (optional) cdf_or_dist* () – distribution to assume if not gaussian. default: scipy.stats.norm xmin, xmax, tol* (*) – only relevant if not gaussian (see xskillscore.crps_quadrature)

Range:

perfect: 1
pos: better than climatology forecast
neg: worse than climatology forecast

References

Matheson, James E., and Robert L. Winkler. “Scoring Rules for Continuous Probability Distributions.” Management Science 22, no. 10 (June 1, 1976): 1087–96. https://doi.org/10/cwwt4g.
Gneiting, Tilmann, and Adrian E Raftery. “Strictly Proper Scoring Rules, Prediction, and Estimation.” Journal of the American Statistical Association 102, no. 477 (March 1, 2007): 359–78. https://doi.org/10/c6758w.

Example

>>> compute_perfect_model(ds, control, metric='crpss')
>>> compute_perfect_model(ds, control, metric='crpss', gaussian=False,
                          cdf_or_dist=scipy.stats.norm, xmin=-10,
                          xmax=10, tol=1e-6)

See also

properscoring.crps_ensemble
xskillscore.crps_ensemble

keyword: 'crpss_es'

climpred.metrics._crpss_es(forecast, reference, **metric_kwargs)[source]¶

CRPSS Ensemble Spread.

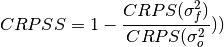
$CRPSS = 1 - \frac{CRPS(\sigma^2_f)}{CRPS(\sigma^2_o}))$

References

Kadow, Christopher, Sebastian Illing, Oliver Kunst, Henning W. Rust, Holger Pohlmann, Wolfgang A. Müller, and Ulrich Cubasch. “Evaluation of Forecasts by Accuracy and Spread in the MiKlip Decadal Climate Prediction System.” Meteorologische Zeitschrift, December 21, 2016, 631–43. https://doi.org/10/f9jrhw.

Range:

perfect: 0
else: negative

keyword: 'brier_score', 'brier', 'bs'

climpred.metrics._brier_score(forecast, reference, **metric_kwargs)[source]¶

Calculate Brier score for forecasts on binary reference.

..math:: BS(f, o) = (f - o)^2

Parameters:	forecast () – reference* () – func* () – function to be applied to reference and forecasts and then mean(‘member’) to get forecasts and reference in interval [0,1]. (required to be added via *metric_kwargs)

Reference:

Brier, Glenn W. “VERIFICATION OF FORECASTS EXPRESSED IN TERMS OF

PROBABILITY.” Monthly Weather Review 78, no. 1 (1950). https://doi.org/10.1175/1520-0493(1950)078<0001:VOFEIT>2.0.CO;2.

Example

>>> def pos(x): return x > 0
>>> compute_perfect_model(ds, control, metric='brier_score', func=pos)

See also

properscoring.brier_score
xskillscore.brier_score

keyword: 'threshold_brier_score', 'tbs'

climpred.metrics._threshold_brier_score(forecast, reference, **metric_kwargs)[source]¶

Calculate the Brier scores of an ensemble for exceeding given thresholds. Provide threshold via metric_kwargs.

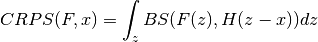
$CRPS(F, x) = \int_z BS(F(z), H(z - x)) dz$

Range:

perfect: 0
min: 0
max: 1

Parameters:	forecast () – reference* () – threshold* () – Threshold to check exceedance, see properscoring.threshold_brier_score (required to be added via *metric_kwargs)

References

Brier, Glenn W. “VERIFICATION OF FORECASTS EXPRESSED IN TERMS OF

PROBABILITY.” Monthly Weather Review 78, no. 1 (1950). https://doi.org/10.1175/1520-0493(1950)078<0001:VOFEIT>2.0.CO;2.

Example

>>> compute_perfect_model(ds, control,
                          metric='threshold_brier_score', threshold=.5)

See also

properscoring.threshold_brier_score
xskillscore.threshold_brier_score

References¶

[EOS]

https://eos.org/opinions/climate-and-other-models-may-be-more-accurate-than-reported

[Jolliffe2011]

(1, 2, 3, 4) Ian T. Jolliffe and David B. Stephenson. Forecast Verification: A Practitioner’s Guide in Atmospheric Science. John Wiley & Sons, Ltd, Chichester, UK, December 2011. ISBN 978-1-119-96000-3 978-0-470-66071-3. URL: http://doi.wiley.com/10.1002/9781119960003.

[Murphy1988]

Allan H. Murphy. Skill Scores Based on the Mean Square Error and Their Relationships to the Correlation Coefficient. Monthly Weather Review, 116(12):2417–2424, December 1988. https://doi.org/10/fc7mxd.