Diagnosing Potential Predictability¶
This demo demonstrates climpred’s capabilities to diagnose areas containing potentially predictable variations from a control or reference alone without requiring multi-member, multi-initialization simulations. This notebook identifies the slow components of internal variability that indicate potential predictability. Here, we showcase a set of methods to show regions indicating probabilities for decadal predictability.
[1]:
import warnings
%matplotlib inline
import climpred
warnings.filterwarnings("ignore")
[2]:
# Sea surface temperature
varname='tos'
control3d = climpred.tutorial.load_dataset('MPI-control-3D')[varname].load()
Diagnostic Potential Predictability (DPP)¶
We can first use the [Resplandy 2015] and [Seferian 2018] method for computing the unbiased DPP by not chunking the time dimension.
[3]:
# calculate DPP with m=10
DPP10 = climpred.stats.dpp(control3d, m=10, chunk=False)
# calculate a threshold by random shuffling (based on bootstrapping with replacement at 95% significance level)
threshold = climpred.bootstrap.dpp_threshold(control3d,
m=10,
chunk=False,
bootstrap=10,
sig=95)
# plot grid cells where DPP above threshold
DPP10.where(DPP10 > threshold).plot(yincrease=False, vmin=-0.1, vmax=0.6, cmap='viridis')
[3]:
<matplotlib.collections.QuadMesh at 0x7fa3315bb908>

Now, we can turn on chunking (the default for this function) to use the [Boer 2004] method.
[4]:
# chunk = True signals the Boer 2004 method
DPP10 = climpred.stats.dpp(control3d, m=10, chunk=True)
threshold = climpred.bootstrap.dpp_threshold(control3d,
m=10,
chunk=True,
bootstrap=50,
sig=95)
DPP10.where(DPP10>0).plot(yincrease=False, vmin=-0.1, vmax=0.6, cmap='viridis')
[4]:
<matplotlib.collections.QuadMesh at 0x7fa331c7e0b8>
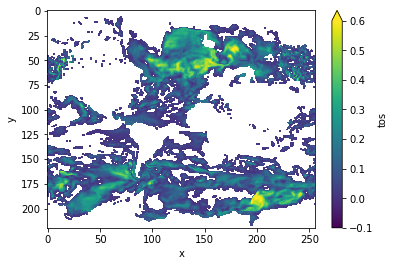
Variance-Weighted Mean Period¶
A periodogram is computed based on a control simulation to extract the mean period of variations, which are weighted by the respective variance. Regions with a high mean period value indicate low-frequency variations with are potentially predictable [Branstator 2010].
[5]:
vwmp = climpred.stats.varweighted_mean_period(control3d, dim='time')
threshold = climpred.bootstrap.varweighted_mean_period_threshold(control3d,
bootstrap=10)
vwmp.where(vwmp > threshold).plot(yincrease=False, robust=True)
[5]:
<matplotlib.collections.QuadMesh at 0x7fa3131b7240>
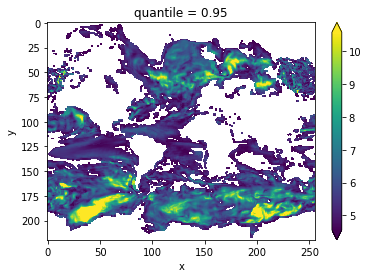
Lag-1 Autocorrelation¶
The lag-1 autocorrelation also indicates where slower modes of variability occur by identifying regions with high temporal correlation [vonStorch 1999].
[6]:
# use climpred.bootstrap._bootstrap_func to wrap any stats function
threshold = climpred.bootstrap._bootstrap_func(climpred.stats.autocorr,control3d,'time',bootstrap=100)
corr_ef = climpred.stats.autocorr(control3d, dim='time')
corr_ef.where(corr_ef>threshold).plot(yincrease=False, robust=False)
[6]:
<matplotlib.collections.QuadMesh at 0x7fa3213b8cc0>
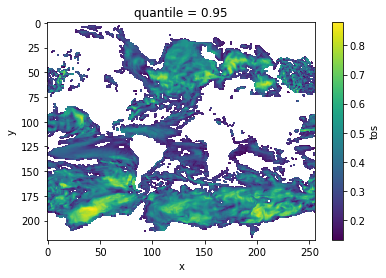
Decorrelation time¶
Taking the lagged correlation further over all lags, the decorrelation time shows the time after which the autocorrelation fell beyond its e-folding [vonStorch 1999]
[7]:
threshold = climpred.bootstrap._bootstrap_func(climpred.stats.decorrelation_time,control3d,'time',bootstrap=100)
decorr_time = climpred.stats.decorrelation_time(control3d)
decorr_time.where(decorr_time>threshold).plot(yincrease=False, robust=False)
[7]:
<matplotlib.collections.QuadMesh at 0x7fa3312afa58>
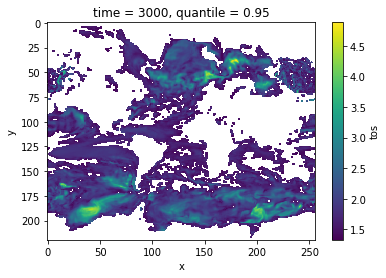
Verify diagnostic potential predictability in predictability simulations¶
Do we find predictability in the areas highlighted above also in perfect-model experiments?
[8]:
ds3d = climpred.tutorial.load_dataset('MPI-PM-DP-3D')[varname].load()
[9]:
bootstrap_skill = climpred.bootstrap.bootstrap_perfect_model(ds3d,
control3d,
metric='rmse',
comparison='m2e',
bootstrap=20)
[10]:
init_skill = bootstrap_skill.sel(results='skill',kind='init')
# p value: probability that random uninitialized forecasts perform better than initialized
p = bootstrap_skill.sel(results='p',kind='uninit')
[11]:
init_skill.where(p<=.05).plot(col='lead', robust=True, yincrease=False)
[11]:
<xarray.plot.facetgrid.FacetGrid at 0x7fa311a2c898>
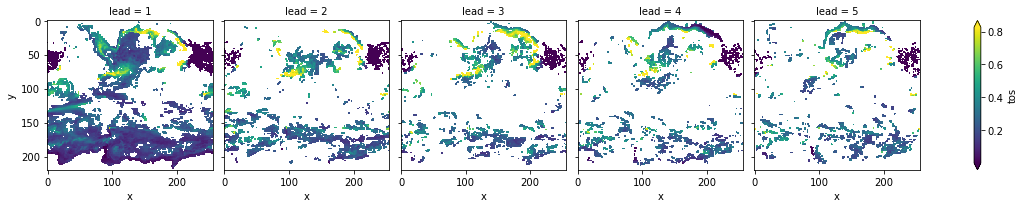
The metric rmse is negatively oriented, e.g. higher values show large disprepancy between members and hence less skill.
As suggested by DPP, the variance-weighted mean period and autocorrelation, also in slight perturbed initial values ensembles there is predictability in the North Atlantic, North Pacific and Southern Ocean in sea-surface temperatures.
References¶
- Boer, Georges J. “Long time-scale potential predictability in an ensemble of coupled climate models.” Climate dynamics 23.1 (2004): 29-44.
- Resplandy, Laure, R. Séférian, and L. Bopp. “Natural variability of CO2 and O2 fluxes: What can we learn from centuries‐long climate models simulations?.” Journal of Geophysical Research: Oceans 120.1 (2015): 384-404.
- Séférian, Roland, Sarah Berthet, and Matthieu Chevallier. “Assessing the Decadal Predictability of Land and Ocean Carbon Uptake.” Geophysical Research Letters, March 15, 2018. https://doi.org/10/gdb424.
- Branstator, Grant, and Haiyan Teng. “Two Limits of Initial-Value Decadal Predictability in a CGCM.” Journal of Climate 23, no. 23 (August 27, 2010): 6292–6311. https://doi.org/10/bwq92h.
- Storch, H. v, and Francis W. Zwiers. Statistical Analysis in Climate Research. Cambridge ; New York: Cambridge University Press, 1999.